1. Bloom Filter

1.1. 一些应用

字处理软件中，需要检查一个英语单词是否拼写正确
在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上
在网络爬虫里，一个网址是否被访问过
yahoo, gmail等邮箱垃圾邮件过滤功能

这几个例子有一个共同的特点：如何判断一个元素是否存在一个集合中？

1.2. 判断一个元素是否存在一个集合中

1、常规思路

数组
链表
树、平衡二叉树、Trie
Map (红黑树)
哈希表

2、问题

虽然上面描述的这几种数据结构配合常见的排序、二分搜索可以快速高效的处理绝大部分判断元素是否存在集合中的需求。但是当集合里面的元素数量足够大，如果有500万条记录甚至1亿条记录呢？这个时候常规的数据结构的问题就凸显出来了。

数组、链表、树等数据结构会存储元素的内容，一旦数据量过大，消耗的内存也会呈现线性增长，最终达到瓶颈。
哈希表效率很高，查询效率可以达到O(1)，但是哈希表需要消耗的内存依然很高。

使用哈希表存储一亿个垃圾 email 地址的消耗？哈希表的做法：首先，哈希函数将一个email地址映射成8字节信息指纹；考虑到哈希表存储效率通常小于50%（哈希冲突）；因此消耗的内存：8 2 1亿字节 = 1.6G 内存，普通计算机是无法提供如此大的内存。

这个时候，布隆过滤器（Bloom Filter）就应运而生。

3、哈希函数

哈希函数：将任意大小的数据转换成特定大小的数据的函数，转换后的数据称为哈希值或哈希编码。

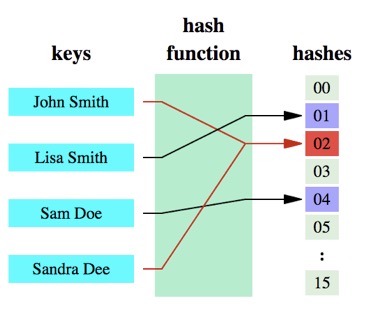
2. 原理介绍

简介：

巴顿.布隆于一九七零年提出
一个很长的二进制向量（位数组）
一系列随机函数 (哈希)
空间效率和查询效率高
有一定的误判率（哈希表是精确匹配）

原理：

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组和几个哈希函数。

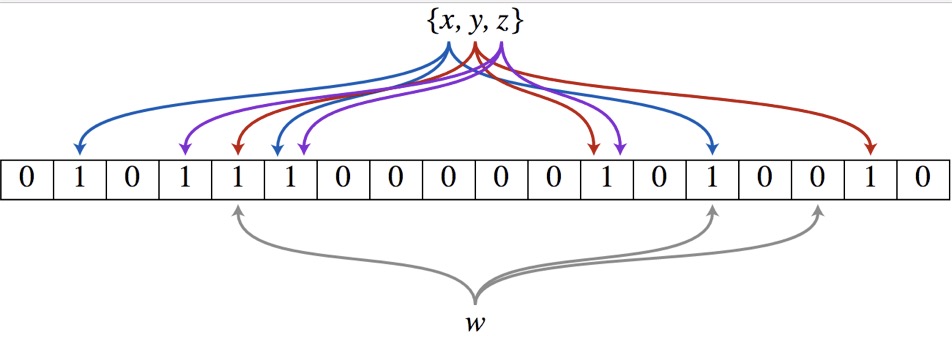
假设集合里面有3个元素{x, y, z}，哈希函数的个数为3。

1、设置

首先将位数组进行初始化，将里面每个位都设置位0。
对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，这个值对应位数组上面的一个点，然后将位数组对应的位置标记为1。

2、查询W元素是否存在集合中

同样的方法将W通过哈希映射到位数组上的3个点。
如果3个点的其中有一个点不为1，则可以判断该元素 一定不存在 集合中。
反之，如果3个点都为1，则该元素 可能存在 集合中。

注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。可以从图中可以看到：假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

2.1. 布隆过滤器添加元素

将要添加的元素给k个哈希函数
得到对应于位数组上的k个位置
将这k个位置设为1

2.2. 布隆过滤器查询元素

将要查询的元素给k个哈希函数
得到对应于位数组上的k个位置
如果k个位置有一个为0，则肯定不在集合中
如果k个位置全部为1，则可能在集合中

部分参考：https://www.cnblogs.com/cpselvis/p/6265825.html

3. 优缺点

1、优点

快速，节省空间，采用位数组，2的32次方=4294967296，可以看到42亿长度的位数组占用 4294967296/8/1024/1024=512MB 只需占用512MB的内存空间

2、缺点

有一定的误判，有可能把不在这个集合中的误判为在这个集合中，所以随着存入集合的元素的增加，误判率也随之增加。

误判率大小和三个指标有关：位数组长度m、集合长度n、散列函数个数k，其之间关系可以参考文献，该文献证明了对于给定的m、n，当 k = ln(2)* m/n ≈0.7 * m/n 时误判率是最小的。

参考资料：https://www.jianshu.com/p/32ed89662d55

一般情况下不能从Bloom Filter中删除元素.

我们很容易想到把位列阵变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在Bloom Filter里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。

3、常见解决方法

常见的补救办法是在建立一个小的白名单，存储那些可能被误判的元素。

4. 复杂度

时间复杂度

添加元素时，由于不需要迭代位数组，而是简单的设置索引位的值，所以操作所花费的时间仅取决于散列函数的个数，所以对于对于k个哈希函数的布隆过滤器，添加元素的时间复杂度为O(k) 。
查询元素时，对于k个哈希函数的布隆过滤器，只需要在位数组中检查的索引数量有一个不变的上界，所以查询元素的时间复杂度也为O(k)。

空间复杂度

由于不需要存储元素，只需依赖一定长度的位数组判断是否存在，并且数组长度的大小不也取决于集合中元素的多少，可以在误判率变大或效率变低的代价下减少存储（位数组）。

5. MurmurHash哈希

MurmurHash是一种非加密型哈希算法，一般用于哈希检索操作。是Austin Appleby在2008年发明的，并出现了多个变种版本，当前版本是MurmurHash3,能够产生出32-bit或128-bit的哈希值。这种哈希算法对于随机分布特征表现更加优良，被广泛运用redis、Hadoop等。

在布隆过滤器中的哈希算法就是采用这种算法。

6. Bitmap

Bitmap在处理海量数据时，有着得天独厚的优势，占用内存非常小（每一个数据只占1个bit），即使在处理url、邮件地址等其他类型的数据时，要把字符串变换为整数，也有各式各样的方法。那么我们为什么不用Bitmap来判重而要用布隆过滤器呢？

首先，我们来看，Bitmap的存储空间计算方式是：找到所有元素里面最大的（假设为N），Bitmap所需空间S为：

S = N/8 Byte

当N为64位整数时，最大的N为2^64，此时S为 2^61 Byte，也就是 2^41 MB，可以说是一个天文数字